인공신경망 - 퍼셉트론을 알아보자.

인공지능의 기초, 퍼셉트론.

 

 

 

오늘은 퍼셉트론에 대해 알아보자.

 

 

오늘의 배움

인공신경망의 기초 개념인 퍼셉트론의 역사와 발전과정 기본 논리 게이트(AND/NAND/OR)의 구현 원리 퍼셉트론의 한계와 다층 퍼셉트론의 등장

---

 

1. 퍼셉트론 (Perceptron)

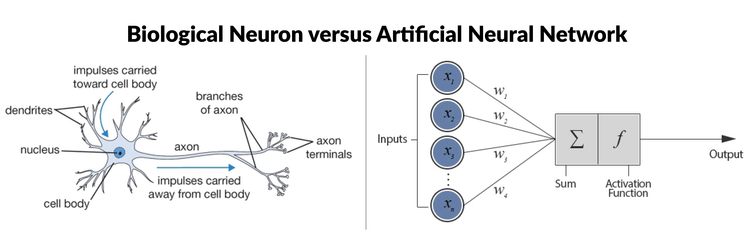
• 정의: 생물학적 뉴런을 모방한 가장 기본적인 인공신경망 모델
• 핵심 개념 한 줄 설명: 입력값에 가중치를 곱하고 편향을 더해 특정 임계값을 넘으면 1, 아니면 0을 출력하는 단순한 인공 신경망

• 퍼셉트론은 선형 모델이다. (입력값과 가중치의 선형 결합에 의해 출력 결정)
• → 단층 퍼셉트론만으로는 XOR와 같은 비선형 문제를 해결할 수 없다.

 

[핵심 공식]: 출력 = f(∑(입력 × 가중치) + 편향)

y = f(w₁x₁ + w₂x₂ + b)
f(x) = 1 if x > 0, else 0
활성화 함수: step function

📚 실제 예시로 이해하기 [일상적인 예시] 식당 방문 결정하기: 가격(x₁)과 맛(x₂)이라는 두 가지 기준 가중치: 가격 중요도(w₁), 맛 중요도(w₂) 편향(b): 기본적인 외식 성향 결과: 식당 방문 여부 결정(0 또는 1) [실무/현업 예시] 이메일 스팸 필터: 특정 키워드 출현 빈도(x₁) 발신자 신뢰도(x₂) 가중치: 각 요소의 중요도 결과: 스팸 여부 판단

---

02.  핵심 개념 정리

• [가중치(Weight)]
  • 정의: 입력값의 중요도를 나타내는 계수
  • 특징: 학습을 통해 조정됨
  • 예시: 시험에서 각 과목의 반영 비율
• [편향(Bias)]
  • 정의: 전체적인 활성화 수준을 조절하는 상수
  • 특징: 임계값 조절 역할
  • 예시: 시험의 가산점
• [활성화 함수(Activation Function)]
  • 정의: 입력신호의 총합을 출력신호로 변환하는 함수
  • 특징: 비선형성 부여
  • 예시: 계단 함수(Step Function)

• [논리 게이트 구현]
  • 정의: 퍼셉트론을 이용한 기본적인 논리 연산 구현
  • 작동 원리: 가중치와 편향을 조절하여 원하는 출력 얻기
  • 특징: AND, NAND, OR 게이트는 단층 퍼셉트론으로 구현 가능
    • AND 게이트: 두 입력이 모두 1일 때만 출력이 1이 된다. 퍼셉트론 모델에서는 가중치와 편향 값을 설정하여 이를 구현할 수 있다.
    • NAND 게이트: AND 게이트의 출력을 뒤집은 형태로, 두 입력이 모두 1일 때만 출력이 0이 된다.
    • OR 게이트: 두 입력 중 하나라도 1이면 출력이 1이 된다.

출처: https://www.researchgate.net/figure/Analogy-between-biological-and-artificial-neuron_fig1_355924918

# AND 게이트 구현
def AND_gate(x1, x2):
    weights = [0.5, 0.5]
    bias = -0.7
    return 1 if (weights[0]*x1 + weights[1]*x2 + bias) > 0 else 0

 

• [다층 퍼셉트론]
  • 정의: 여러 층의 퍼셉트론을 연결한 신경망 구조
  • 작동 원리: 은닉층을 통해 비선형 문제 해결 ->  복잡한 패턴을 학습할 수 있음
  • 특징: XOR 문제 해결 가능

출처: https://www.datacamp.com/tutorial/multilayer-perceptrons-in-machine-learning

[참고] XOR (Exclusive OR, 배타적 논리합)이란

두 개의 비트가 서로 다를 때 1, 같을 때 0을 반환하는 논리 연산이다.

A	B	A ⊕ B
0	0	0
0	1	1
1	0	1
1	1	0

⇒ 이를 극복하기 위해 비선형 활성화 함수와 다층 구조가 필요하다.

# XOR 게이트 구현 (다층 퍼셉트론 사용)
from sklearn.neural_network import MLPClassifier

mlp = MLPClassifier(hidden_layer_sizes=(2,))
X = [[0,0], [0,1], [1,0], [1,1]]
y = [0, 1, 1, 0]
mlp.fit(X, y)

 

비교분석표

구분	단층 퍼셉트론	다층 퍼셉트론
구조	입력층, 출력층	입력층, 은닉층, 출력층
해결가능 문제	선형 분리 가능 문제	비선형 문제
대표적 구현	AND, OR 게이트	XOR 게이트
학습방식	단순 학습 규칙	역전파 알고리즘

 

 

---

 

[코드 총정리]

import numpy as np
import matplotlib.pyplot as plt

class Perceptron:
    def __init__(self, learning_rate=0.1, n_iterations=100):
        self.learning_rate = learning_rate
        self.n_iterations = n_iterations
        self.weights = None
        self.bias = None
        
    def fit(self, X, y):
        n_samples, n_features = X.shape
        self.weights = np.zeros(n_features)
        self.bias = 0
        
        for _ in range(self.n_iterations):
            for idx, x_i in enumerate(X):
                linear_output = np.dot(x_i, self.weights) + self.bias
                y_predicted = self.activation_function(linear_output)
                
                # 가중치 업데이트
                update = self.learning_rate * (y[idx] - y_predicted)
                self.weights += update * x_i
                self.bias += update
    
    def predict(self, X):
        linear_output = np.dot(X, self.weights) + self.bias
        return self.activation_function(linear_output)
    
    def activation_function(self, x):
        return np.where(x >= 0, 1, 0)

# 논리 게이트 구현 및 테스트
def test_logic_gates():
    # 학습 데이터 준비
    X = np.array([[0,0], [0,1], [1,0], [1,1]])
    
    # AND 게이트
    y_and = np.array([0,0,0,1])
    perceptron_and = Perceptron()
    perceptron_and.fit(X, y_and)
    print("AND Gate 결과:", perceptron_and.predict(X))
    
    # OR 게이트
    y_or = np.array([0,1,1,1])
    perceptron_or = Perceptron()
    perceptron_or.fit(X, y_or)
    print("OR Gate 결과:", perceptron_or.predict(X))
    
    # NAND 게이트
    y_nand = np.array([1,1,1,0])
    perceptron_nand = Perceptron()
    perceptron_nand.fit(X, y_nand)
    print("NAND Gate 결과:", perceptron_nand.predict(X))

    # 결정 경계 시각화
    plt.figure(figsize=(15, 5))
    
    gates = ['AND', 'OR', 'NAND']
    perceptrons = [perceptron_and, perceptron_or, perceptron_nand]
    
    for idx, (gate, perceptron) in enumerate(zip(gates, perceptrons)):
        plt.subplot(1, 3, idx+1)
        
        # 결정 경계 그리기
        x_min, x_max = -0.5, 1.5
        y_min, y_max = -0.5, 1.5
        xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
                            np.linspace(y_min, y_max, 100))
        Z = perceptron.predict(np.c_[xx.ravel(), yy.ravel()])
        Z = Z.reshape(xx.shape)
        
        plt.contourf(xx, yy, Z, alpha=0.4)
        plt.scatter(X[:,0], X[:,1], c=['red' if label else 'blue' for label in eval(f'y_{gate.lower()}')])
        plt.title(f'{gate} Gate')
        plt.xlabel('Input 1')
        plt.ylabel('Input 2')
    
    plt.tight_layout()
    plt.show()

# 실행
test_logic_gates()

 

---

 

생물학적 뉴런과 인공뉴런의 모습이 유사함에 있어 흥미로웠다.

다양한 활성화 함수에 대해 알아보자.